Forskning* viser at fysiske aktiviteter i undervisningen virker positivt på læring. Dette fordi barn lærer mens de er i bevegelse, som igjen skaper flere koblinger i hjernen. På denne måten får elevene en dypere og mer omfattende forståelse, når kroppen også er med på læringen. Ragnhild Øksdahl, matematikklærer ved Nord-Odal ungdomsskole, er opptatt av aktiv læring, forenkling av matematikk og har stor tro på at veien til dypere forståelse går gjennom utforsking og problemløsning.
Den tiden hvor læreren stod foran tavla og foreleste mens elevene skrev side opp og ned med formler, for så pliktoppfyllende å anvende disse, er snart over, håper og tror Ragnhild. Hun mener at matematikkundervisningen nå står foran et skifte. Mange matematikklærere i dag jobber med å flytte fokus fra drilling til forståelse, samt legge grunnlag for at elevene skal jobbe mer utforskende. Dette kan skape noen gnisninger blant elevene, spesielt på ungdomsskolen.
Elevene fra barneskolen er mer vant til å jobbe etter “kokebok oppskrift” metoden. Ragnhild tror ikke disse utfordringene blir vedvarende nå som flere og flere lærere, også på barneskolen, setter fokus på utforsking og problemløsning. Det er viktig å huske på at læreplanen tross alt bare er to år gammel, minner hun om.
Utforskende læring - elevene oppdager matematikken selv

Noe Ragnhild synes er fint, som elevene også synes er engasjerende og motiverende, er når de jobber med problemløsning. Hun liker spesielt de gode og rike problemene med lav inngangsterskel som gjør det lett å komme i gang for de fleste elever, samtidig som det er mulig å jobbe på et svært høyt matematisk nivå. Her kan alle bidra i arbeidet etter egne evner. Hun forteller om en økt hun gjennomførte, som skapte mye engasjement hos elevene.
– Problemoppgaven handlet om en rubiks kube som vi hadde malt på utsiden for så å dele den opp i mindre kuber. Så fikk elevene i oppgave å finne ut hvor mange sider har 3 sider malt, hvor mange har 2 sider malt, én side og ingen sider. Så utvidet vi problemstillingen ved å spørre om hvordan det er for en kube med 4 x 4 x 4 og en med 5 x 5 x 5? Til slutt hvordan er det for en kube med n x n x n? forteller hun.

Dette er en typisk LIST-oppgave (LIST = Lav Inngangsterskel, Stor Takhøyde). For å sikre deltakelse av de mindre aktive elevene hadde hun med seg konkreter i form av Multi klosser. Elevene jobbet på vertikale tavler etter Peter Liljedahl sin didaktikk «Building thinking classroom». Liljedahls teori fastsetter at hvis elevene kan skrive på en tavle som lett kan viskes ut, blir terskelen for å skrive lavere. For denne oppgaven hadde ikke Ragnhild gitt noen instruks, slik at elevene hadde valgfrihet når det gjaldt metodebruk.
Oppgaven var en god kombinasjon av utforskende problemløsning, aktiv læring og visualisering ved bruk av konkreter:
– Det som skjedde i løpet av denne økten er at elevene kom i gang ganske fort, og at de på egen hånd prøvde å systematisere og strukturere informasjon, blant annet ved å sette opp tabeller. For meg som lærer var det veldig givende og gøy å se på! sier Ragnhild.
Men utfordringen, fortsetter hun, er at den måten å jobbe på er tidkrevende:
– Vi brukte to timer på denne oppgaven. Som lærer kan jeg ofte føle press på å gå gjennom pensum, sier hun i tillegg.
Forenkling av matematikk hjelper med forståelse
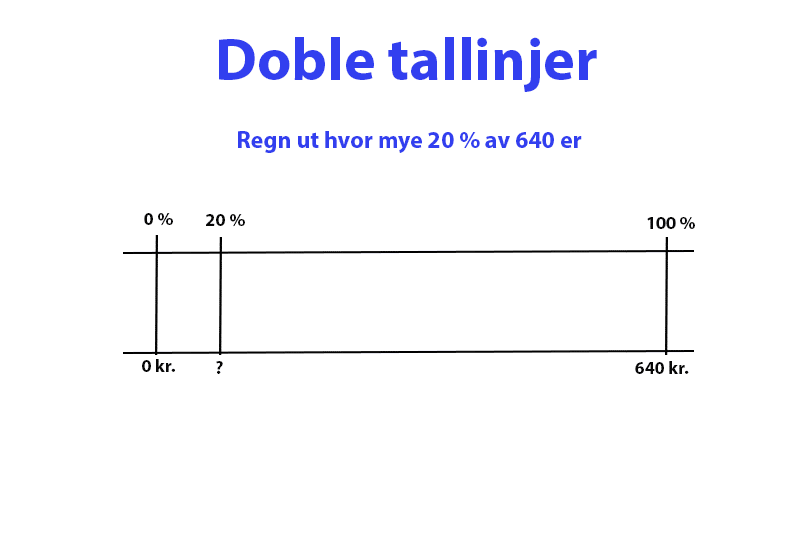
En annen ting Ragnhild tar opp, er at hun er opptatt av forenkling av matematikk. Hun vil at eleven skal tenke forenkling, lære og utvikle strategier og snarveier, slik at det å regne blir enklere. Det handler om å hjelpe dem med å finne gode hoderegningsstrategier som funker for dem.
– Jeg sier til elevene: når du skal dele på 8 for eksempel, kan du jo tenke halvparten av halvparten av halvparten. Jobber vi med prosent med elever som strever, bruker jeg ofte doble tallinjer for å vise det. Så jeg tegner en del, for forenkling er å tegne og! Spesielt for denne elevgruppen. Jeg vil at de skal forstå, og alt jeg driver med i mattetimen bygger under det at elevene skal forstå, forteller hun.
Når jeg spør om hun har et eksempel på hvor det kan være lurt å tenke forenkling, forteller hun om en oppgave hun fortalte en kollega:
– Ola er på sykkeltur i skogen. Han sykler 3 kilometer på 20 minutter, hva blir gjennomsnittsfarten hans? spør hun.
I det kollegaen begynner å dra fram “trekanten” for vei, fart og tid, svarer hun:
– Ola sykler 3 kilometer på 20 minutter, dvs. 6 kilometer på 40 minutter og 9 kilometer på 60 minutter. Gjennomsnittsfarten er da 9 km/t, forklarer hun. Det trengs ikke å gjøres mer komplisert enn det. Forenklingen hjelper med forståelsen og sikrer at elevene logisk kan resonnere seg fram til et resultat og huske det!