I Kikora har vi tro på at en utforskende tilnærming til matematikken gjør elevene til bedre problemløsere. Gjennom å oppdage sider av fagstoffet på egenhånd og uttrykke oppdagelsene sine, blir elevene bedre rustet til å bryte nye problemer ned til mindre delproblemer og analysere disse hver for seg.
Når elevene settes i en situasjon der de skal utforske er det likevel viktig at det finnes en konkret plan for hva elevene skal oppdage – det må ikke kun bli utforskning for utforskingens del, men ende opp i noe konkret de kan ta med seg videre. Derfor krever utforskningen noen rammer og struktur.
Et tema vi mener er et godt utgangspunkt for utforskning, er andregradsfunksjoner. Her kan elevene oppdage egenskaper og generaliserbare sammenhenger som de kan ta med seg videre inn i arbeidet med disse funksjonene. I kompetansemålene for 1T er også utforskning nevnt eksplisitt i forbindelse med andregradsfunksjoner:
“utforske samanhengar mellom andregradslikningar og andregradsulikskapar, andregradsfunksjonar og kvadratsetningane og bruke samanhengane i problemløysing”
Interaktiv utforskning av andregradsfunksjoner
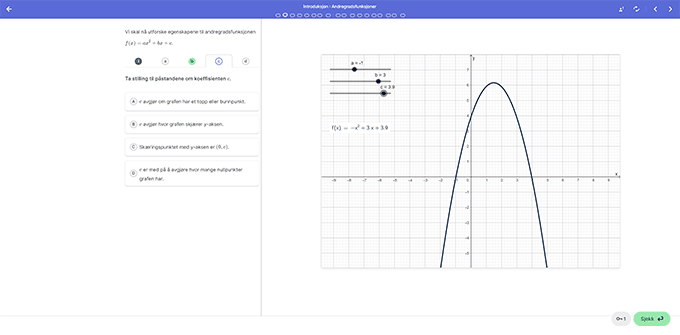
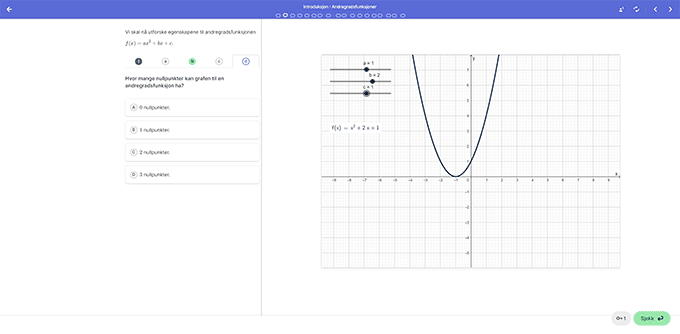
I Kikora kan elevene settes rett inn i en interaktiv og utforskende kontekst. I eksempelet som bildene under er hentet fra skal elevene først utforske egenskapene til koeffisientene a, b og c i et generelt andregradsuttrykk ved å endre verdiene ved hjelp av glidere, og notere ned egne observasjoner så presist som mulig.
Deretter blir elevene bedt om å ta stilling til en rekke påstander knyttet til de tre koeffisientenes egenskaper. På denne måten veiledes elevenes utforskning i en retning som øker elevenes forståelse. I og med at oppgavene er dynamiske, kan elevene stadig endre og prøve ut på nytt når de oppdager nye sammenhenger eller andre ting som de ønsker å undersøke.



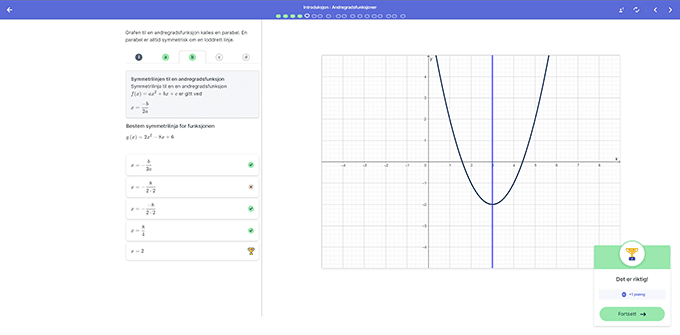
Sammenhengen mellom andregradsfunksjoner og andregradslikninger
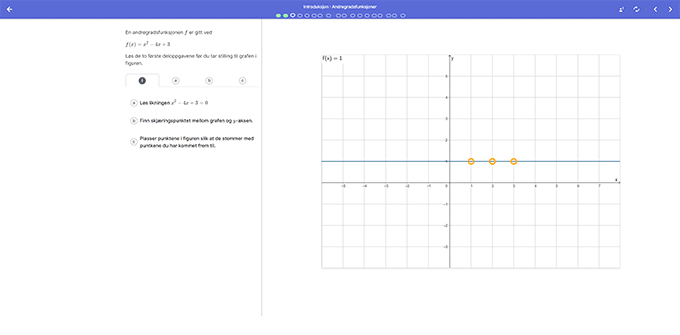
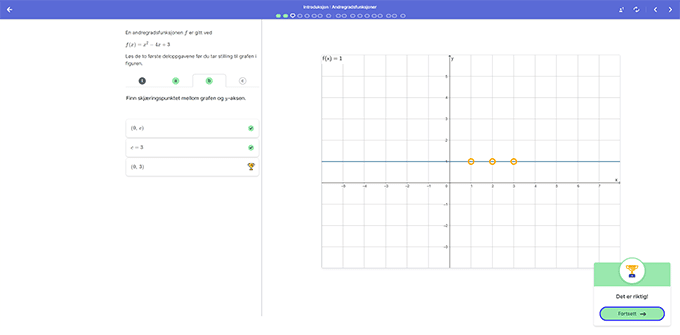
I de påfølgende oppgavene knyttes egenskapene ved grafen til en andregradsfunksjon sammen med andregradslikninger som elevene allerede har lært å løse. Her er hensikten at elevene skal koble sammen det algebraiske og grafiske aspektet, og ta i bruk noen av de generelle sammenhengene de oppdaget i utforskningen.
Dette gjør de først gjennom å studere et funksjonsuttrykk og avgjøre egenskaper ved grafen. Deretter skal de resonnere motsatt vei ved å avgjøre egenskaper ved funksjonsuttrykket basert på grafen. I arbeidet med likninger og algebraiske uttrykk får elevene kontinuerlig feedback på utregningene de gjør, og det blir enkelt å identifisere hvor eventuelle regnefeil oppstår





Er nullpunktene symmetriske?
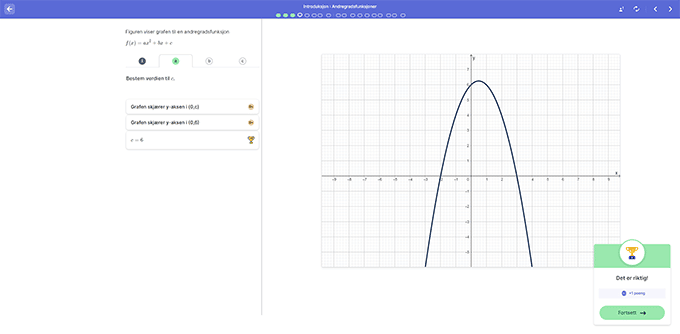
Videre ser elevene på sammenhenger mellom nullpunkt og symmetrilinje for andregradsfunksjoner, og må igjen ta stilling til påstander som er med på å avgrense begrepsbildet deres.
Dersom elevene står fast i regneoppgavene og ikke kommer videre finnes det også løsningsforslag, der elevene kan klikke seg igjennom hvert enkelt steg for å se hvordan utregningene skal gjøres og hvor de eventuelt har gjort feil. De velger selv hvor mye hjelp de vil ha i form av antall nøkler.




Å koble sammen trådene
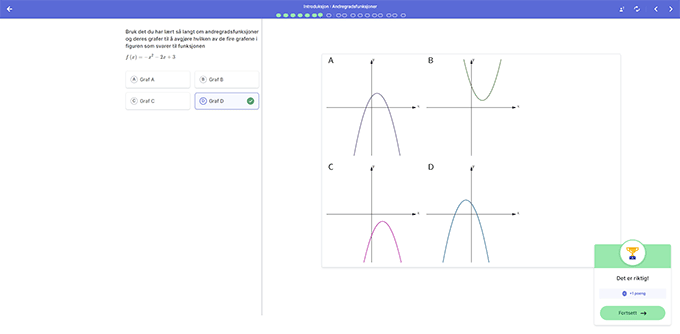
Avslutningsvis må elevene ta i bruk alle egenskapene de har sett på for andregradsfunksjoner for å avgjøre hvilken graf som kan passe med funksjonsuttrykket de blir presentert for. Hensikten her er at hver egenskap de tidligere har sett på kan være med å utelukke en av grafene frem til de står igjen med den riktige. Slik får elevene satt sammen det de har utforsket og lært fra før i de tidligere oppgavene.