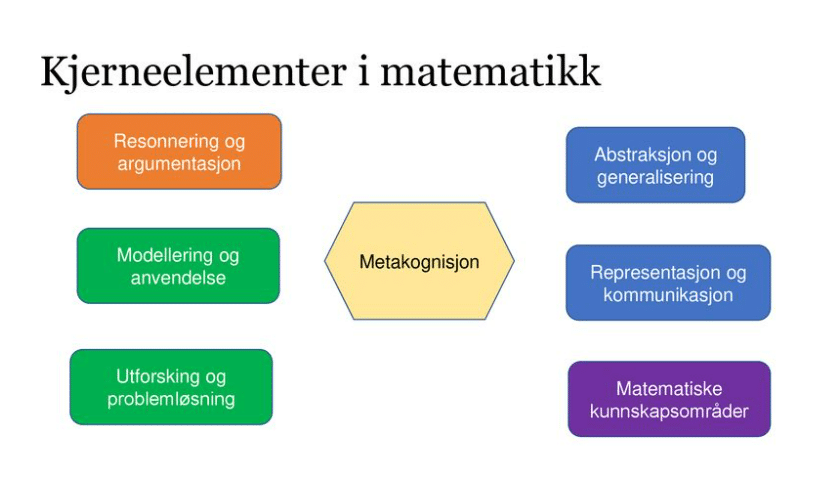
Oppgavene og de såkalte læringspakkene i Kikora bygger opp under samtlige kompetansemål som vi finner i matematikk i LK20. Samtidig er innholdet strukturert slik at oppgavene i en læringspakke naturlig kommer innom de ulike kjerneelementene. Det betyr at når elevene jobber med Kikora vil de naturlig være innom kjerneelementene i matematikk. Dette fører forhåpentligvis til at elevene blir bedre problemløsere og samtidig forstår hvordan matematikk henger tett sammen med andre fag.

Utforsking og problemløsning
Vår opplæring bygger opp om LK-20 sin filosofi hvor elevene er aktive og undersøkende i sine læringsprosesser. I Kikora er derfor mange av oppgavene av en slik art at de innbyr til utforsking og problemløsing. Vi retter ikke fokus mot kun en riktig fremgangsmåte, men lar gjerne elevene jobbe med oppgaver og aktiviteter som har en mer undersøkende tilnærming. Dette viser seg å ha betydning for elevens motivasjon, som viser seg å øke når elevene får en undersøkende tilnærming til matematikk. Elevens motivasjon og følelse av mestring var større når de fikk arbeide med aktiviteter hvor de fikk mulighet til å utvikle forståelse i matematikk. Elevens følelse av læring og forståelse var nær knyttet til at de fikk være delaktige i å utvikle egne løsningsstrategier og metoder i faget. (Kjersti Wæge, 2007).
I mange av oppgavene som du finner i Kikora, så finnes det derfor ikke én riktig framgangsmåte for å løse oppgavene. Her er det muligheter for å prøve seg fram for å finne mønster, sammenhenger og egne løsninger på problemene. Tett fulgt av vår unike mattemotor, som faktisk forstår elevenes ulike fremgangsmåter, får elevene kontinuerlig tilbakemelding linje for linje. Det betyr at dersom elevenes tanker om mulig fremgangsmåte er feil, så blir de stoppet i det feilen inntreffer. Dette begrenser muligheten for at elevene øver seg på eventuelle misforståelser. Videre tenker vi det er på sin plass å utfordre elevene til å tenke kreativt og systematisk i dette arbeidet, da det å vurdere ulike framgangsmåter og løsninger er en essensiell del av læringsarbeidet.
Modellering og anvendelser
Modellering i matematikk handler om hva man kan bruke matematikk til ute i virkeligheten, ved å lage modeller som beskriver situasjonen med et matematisk språk. En del oppgaver i Kikora vil egne seg godt til å utvikle matematiske modeller og vurdere om modellene er gyldige og hvilke begrensninger de har.
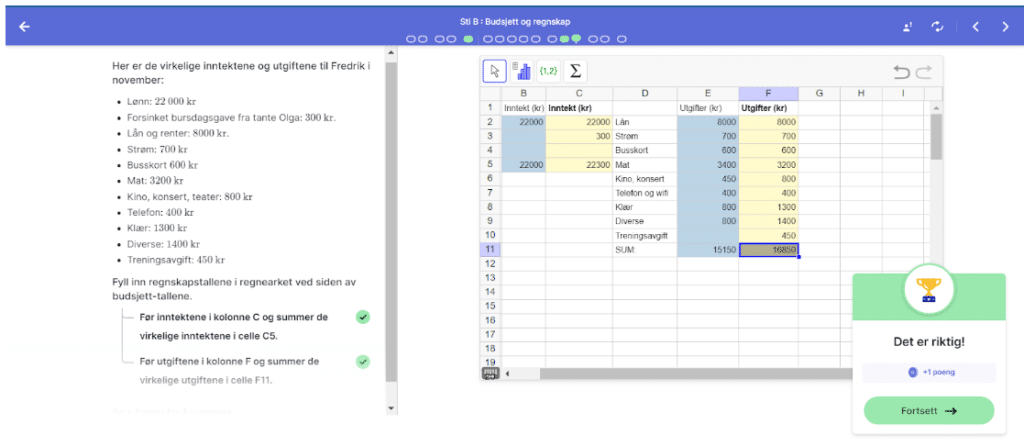
Uansett hvilke oppgaver elevene arbeider med, så vil de ha mulighet til å ta i bruk det de kan og vet fra før. De får også innsikt i hvordan vi anvender matematikk i ulike situasjoner. Ved å bruke kunnskap og ferdigheter de allerede har (elevens bakgrunnskunnskap) for å løse oppgaver i kjente og ukjente sammenhenger kan elevene utvikle sin kompetanse i faget.


Resonnering og argumentasjon
Resonnering i matematikk handler om å kunne følge, vurdere og forstå matematiske tankerekker. Det innebærer at elevene skal forstå at matematiske regler og resultat ikke er tilfeldige, men har klare begrunnelser. Elevene skal utforme egne resonnement både for å forstå og for å løse problem. Argumentasjon i matematikk handler om at elevene begrunner sine fremgangsmåter, resonnement og løsninger og beviser at disse er gyldige. I matematikk må elevene stadig resonnere og argumentere underveis i arbeidsprosessen, og de må vurdere om framgangsmåten de har valgt fører dem mot en løsning.
Representasjon og kommunikasjon
Representasjoner i matematikk er måter å uttrykke matematiske begrep, sammenhenger og problemer på. Representasjoner kan være konkrete, kontekstuelle, visuelle, verbale og symbolske. Kommunikasjon i matematikk handler om at elevene bruker matematisk språk i samtaler, argumentasjon og resonnement.

Elevene må få mulighet til å bruke matematiske representasjoner i ulike sammenhenger gjennom egne erfaringer og matematiske samtaler. Elevene må få muligheten til å forklare og grunngi valg av representasjonsform. Elevene må kunne skille mellom matematiske representasjoner og dagligspråket og veksle mellom ulike representasjoner.

I Kikora er det en stor fordel om elevene får samarbeide om løse oppgaver. Det vil gi dem muligheter til å kommunisere både skriftlig og muntlig underveis, de må lytte til hverandre og prøve å forstå og vurdere hverandres bidrag. Det at elevene selv får velge hvordan de vil notere og presentere arbeidet sitt gir rom for bruk av ulike representasjoner, og klassen kan ved hjelp av diskusjonsoppgavene i Kikora samtale om hvilke representasjoner som til enhver tid egner seg best.
Abstraksjon og generalisering
Abstraksjon i matematikk innebærer at elevene gradvis utvikler en måte som formaliserer tanker, strategier og et matematisk språk. Utviklingen går fra konkrete beskrivelser til et formelt symbolspråk og formelle resonnement.
Generalisering i matematikk handler om at elevene oppdager sammenhenger og strukturer uten at de blir presentert for en ferdig løsning. Det vil si at elevene kan utforske tall, utregninger og figurer for å finne sammenhenger og deretter formalisere ved å bruke algebra og formålstjenlige representasjoner.

Når elever utforsker variasjonene i oppgavene vil de kunne oppdage sammenhenger og strukturer som er mer allmenngyldige enn kun for det aktuelle eksemplet de arbeider med. I kladdeboka kan de representere med tegninger, tabeller eller symboler, mens de i Kikora etter hvert kan formalisere gjennom bruk av algebra. Elevene abstraherer og generaliserer arbeidet sitt. Elever både på 1. trinn og på vg2 kan generalisere arbeid på en slik måte.