I Kikora tror vi på en utforskende tilnærming til nytt fagstoff. Når vi lager forklarende innhold, bruker vi ikke tekster, eksempler eller videoer, men lager heller modeller og visualiseringer for å konkretisere matematikken. Alle nyere læreverk på papir har slike figurer og illustrasjoner. Kikora har også dette, men i tillegg er det integrert dynamiske og interaktive modeller som i større grad lar eleven utforske og oppdage på sitt nivå, og i sitt eget tempo.
Arealmodellen er ett eksempel på en slik grunnleggende modell, og denne er mye brukt i klasserom over hele verden, på ulike trinn – så også i Kikora. En elev som jobber med Kikora fra barneskolen til videregående, vil derfor møte denne, og tilsvarende modeller, igjen og igjen.
Arealmodellen kan hjelpe elever på barnetrinnet med å forstå enkel multiplikasjon, elever på mellomtrinnet å forstå multiplikasjon med flersifrede tall, elever på ungdomstrinnet å forstå faktorisering, og elever på videregående å løse andregradslikninger eller utføre polynomdivisjon.
Videre følger noen eksempler fra Kikora katapult. Eksemplene kan i høyeste grad også være relevante for elever på andre trinn enn det er vist til her, ettersom alle klasser har elever som befinner seg på et faglig nivå over eller under klassetrinnet de hører til. Med Kikora får alle elever tilgang til alt innholdet, slik at man i større grad kan tilpasse nivået også til elevene som befinner seg i de faglige ytterpunktene.
Barnetrinnet
Elevene utforsker multiplikasjon gjennom å manipulere figurene og få tilbakemelding fra Kikora på at de har laget gangestykker hvor arealet er 12 ruter. Da vil de sannsynligvis også på egenhånd oppdage den kommutative lov, altså at faktorenes orden er likegyldig, f.eks. 4*3=3*4.
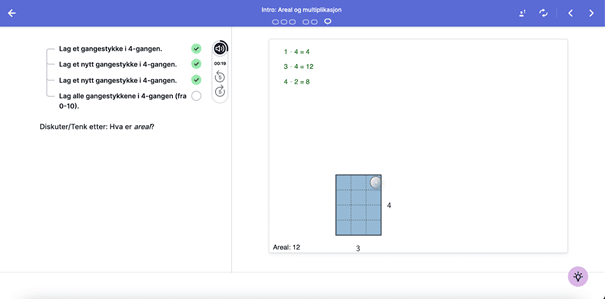
Mellomtrinnet
Multiplikasjon med flersifrede tall: Her kan elevene utforske ulike strategier for å dele opp et stykke slik at utregningen blir meningsfull. Visualiseringen kan også gi elevene en strategi for hoderegning i tilsvarende oppgaver. Dette i motsetning til å pugge en algoritme som for mange gir mekanisk ferdighet og liten matematisk forståelse. Dermed vil elevene også kunne oppdage den distributive lov.
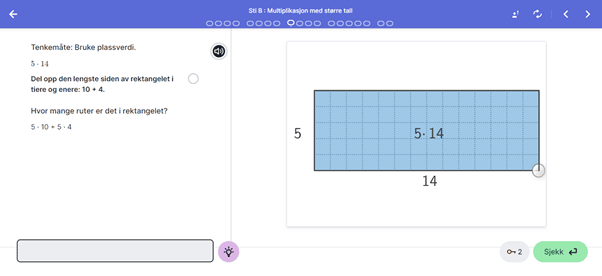
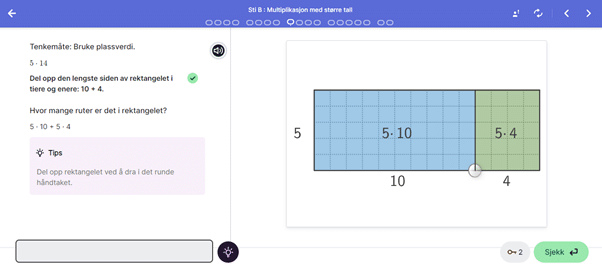

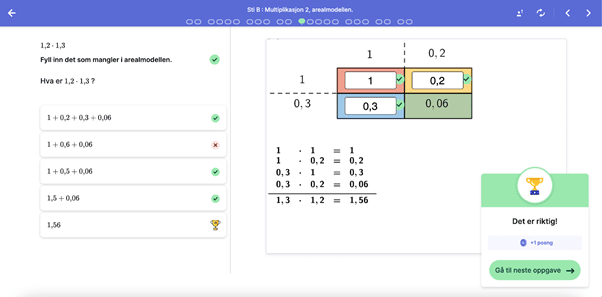
Multiplikasjon med desimaltall kan også gjøres mer forståelig med arealmodellen.
Ungdomstrinnet
Et eksempel fra ungdomstrinnet er faktorisering. Her brukes arealmodellen både med og uten rutenettet. Nedenfor er et eksempel uten. Fargene skal hjelpe elevene ytterligere til å se sammenhengen mellom variantene med og uten rutenett.


Videregående
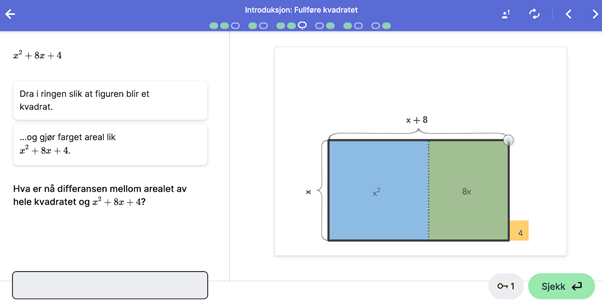
Et eksempel fra videregående er fullstendige kvadraters metode. Modellen som hjelper 7-åringen med å forstå multiplikasjon av ensifrede tall, kan også hjelpe 17-åringen med å forstå faktorisering av andregradsuttrykk med kvadratsetningene. Erfaringsvis er sistnevnte noe som for mange kun er en mekanisk operasjon, med liten grad av faktisk forståelse for hva man gjør og hvorfor.
Arealmodellen kan hjelpe flere med å holde styr på hva som skjer underveis i beregningene, og gi elevene et bilde de kan ta med seg videre og bruke også når de ikke rent faktisk har den foran seg på skjermen.


Et annet eksempel fra videregående er polynomdivisjon. For mange elever vil det å fylle inn i modellen gi bedre forståelse for hvilke regneoperasjoner som må gjøres, og hvorfor. Som eksempelet på bildet under viser, får eleven ofte hjelp til å forstå hvordan å bruke en modell, gjennom trinnvise instruksjoner.
Etter hvert bruker eleven modellen på egenhånd, og i en del tilfeller – utover i gjøremålet – står modellen der som en hjelp for de som ønsker det.