10 aktiviteter som forener matematikklæring og fysisk aktivitet. Aktivitetene er hentet fra én ukes sommerskole på Lillebru Gård for mellomtrinnet, men aktivitetene kan tilpasses både barnetrinnet og ungdomstrinnet. Matematikkøktene er laget av Anders Baumberger på oppdrag fra Landslaget for matematikk i skolen (LAMIS).
Matematikkøkt 7: Vekt og volum til det man støter på
Overalt møter vi på ting som elever flest ikke engang tenker at det er mulig å regne på. Spesielt ikke i hodet. Vis at det umulige kan være ganske enkelt, selv uten noe annet enn hodet, dersom man aksepterer at det er anslag og ikke presisjon som er målet.
Ofte holder det å kikke ut av vinduet i klasserommet:
- Hvor mange trær er det på det fjellet.
- Hvor mange mennesker får plass på skolegården.
- Hvor mye veier jordkloden?
- Hvor lang tid tar det å ta bussen til månen?
- Hvor mye veier denne steinen?
- Hvor mange liter vann er det i dette vannet?
- Hvor mange øyevipphårstrå er det i verden?
- Hvor mange hårstrå har hunden min?
- Hvor lenge kan jeg fyre med dette ene treet her?
Mulighetene er uendelige. Det er viktig at det er elevene selv som stiller spørsmålene, men ofte trenger de litt hjelp til å bli kreative nok til å i det hele tatt komme opp med spørsmålene.
Et eksempel på hvor mye vi av og til forenkler. Tjernet på videoen som vi estimerte til 6 milliarder liter vann var basert på et enkelt anslag om gjennomsnittlig lengde, bredde og dybde. Når vi senere sjekket arealet til vannet på norgeskart.no ved å måle opp nokså nøyaktig, fikk vi med samme dybdeanslag et volum på ca 6,5 milliarder liter. Videre er det enkelt å si at «dersom vi har bommet på gjennomsnittlig dybde med så så mange meter, så påvirkes svaret tilsvarende.

Matematikkøkt 8: Lydhastighet – et bokstavelig talt utrolig eksperiment
Stålsett deg nå: Er det mulig å oppleve en hendelse «live» ETTER at man har hørt om akkurat denne hendelsen i nyhetene? Spørsmålet virker absurd, men svaret er (I visse situasjoner knyttet til lyd), altså JA.
Mange elever tar ikke innover seg hvor utrolig treg lyden egentlig er. I alle fall sammenliknet med lyshastigheten. Ta elevene med til et utkikkspunkt, eller gjør motsatt, se opp til en topp eller ut til en øy veldig langt unna. Helst flere mil unna.
Skap et scenario der en rakett eller liknende eksploder der borte, og start stoppeklokka idet eksplosjonen finner sted. Elevene rekker så opp hånda når de tror lyden når fram til dem.
I eksempelet i videoen gjettet elevene mellom 0 og 8 sekunder, mens svaret som kjent er ca 3 sekunder per kilometer, som gir over 4 minutters reisetid for lyden med over 80 km sikt. Med andre ord mer enn nok tid til at man kan skru på radioen for å høre siste nytt om eksplosjonen. Eller venner og kjente som bor I nærheten av eksplosjonsstedet kan ringe og fortelle at «nå passerte lyden forbi oss, og om noen minutter vil den nå dere».
Matematikkøkt 9: Massen til en sky
Luft har overraskende høy masse! Faktisk ca 1 kg pr kubikkmeter luft. Så, hvor stor masse har lufta i klasserommet? I skolegården?
For eldre elever:
Hva med en sky? Tordenskyen på videoen definerte vi nokså forenklet som en sylinder med en anslått radius på 2 km og en høyde på 10 km. Enkelt geometri og hoderegning (igjen der pi er 3), gir et volum på 120 kubikkilometer.
Så hvor mange kubikkmeter går det pr kubikkilometer?
Jo 1000x1000x1000. Altså én milliard kubikkmeter, som da gir en masse på én milliard tonn.
Vår sky har altså en estimert masse på 120 millioner tonn, som tilsvarer massen til 120 millioner biler. Hvem hadde trodd det?…
Matematikkøkt 10: Hva er 0D og 1D? Figurjakt.
Denne økta begynner jeg gjerne med en prat om 3D. Elevene henger med. Da kommer også 2D etter hvert. Men hva er 1D? Og 0D? Etter en prat om teorien bak, og noen aha-opplevelser om hvor 2- og 3-tallet kommer fra i benevningen for kvadratmeter og kubikkmeter, så tar vi det praktiske.
Be elevene gå på jakt etter figurer i virkeligheten. For hver figur skal de angi det matematiske navnet til figuren, om det er 1D, 2D eller 3D og skrive opp hva det er i virkeligheten.
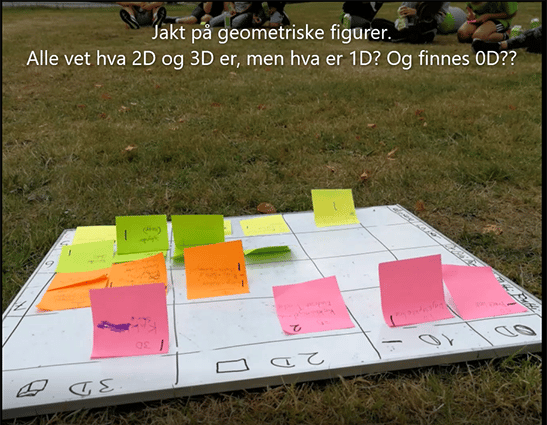
Eks:
Rektangel : 2D Vindu
Det kan argumenteres for at de fleste/alle gjenstander i virkeligheten er 3D og det gir mulighet for gode samtaler. Eksempelvis kan jeg si: Jeg kan akseptere at du setter dette som 2D dersom du argumenterer godt for at det kan defineres slik. Hva legger du til grunn for å hevde at det er 2D og ikke 3D. Vi er jo alltid ute etter de gode ressonementene som viser forståelse, mer enn å forsøke å argumentere for at et vindu egentlig er 3D.