I november gjennomførte vi i Kikora en kursdag i samarbeid med Ålesund kommune. Sammen med Hallgeir Buset, ass. rektor på Blindheim ungdomsskole, arrangerte vi også en læringsøkt på kvelden hvor vi rettet fokus mot Kikoras problemløserskole og Peter Liljedahls forskning om vertikale tavler og tenkende klasserom.
Hvorfor problemløsning?
Det å arbeide med problemløsning er tidkrevende, men det er det absolutt verdt, ifølge Hallgeir Buset. Han innledet sin del av kurskvelden med å beskrive egen undervisningspraksis.
– Dersom jeg som lærer legger opp til å undervise i fremgangsmåter og prosedyrer i stedet for at elevene får utvikle innsikt, er det de individuelle øvingene som vektlegges.
Hallgeir beskriver en tradisjonell mattetime jeg tror mange kjenner seg igjen i. Læreren går gjerne gjennom litt teori og viser et par eksempler på tavla, før elevene fortsetter å gjøre oppgaver fra læreboka. Eventuelt hjemmearbeid fortsetter i samme tralten. Kort oppsummert er det ikke unormalt at en mattetime blir slik.
«Presset læreren føler på «å komme gjennom boka» fører til at læreren setter av for lite tid til samtale og diskusjon. Men det er nettopp disse samtalene og diskusjonene – og ikke mengden av løste oppgaver – som sikrer dybdelæringen hos elevene.» (Van Galen m. fl., 2008). Deltakerne fikk derfor reflektere rundt problemstillingen: «Hvor stor del av en slik tradisjonell time har elevene fått mulighet til å tenke selv?»

Å få tid til å arbeide med problemløsningsaktiviteter bidrar derfor til økt forståelse og dybdelæring hos elevene. Tom Rune Kongelf ved Høgskulen på Vestlandet – campus Sogndal, peker på at land som gjør det godt i matematikk har et sterkt fokus på problemløsing.
«Rammeverket for læreplanen i Singapore betrakter problemløsing som kjernen i matematikkundervisningen, og lærebøkene vier hele kapitler på problemløsing med fokus på heuristikk – spesifikke strategier for problemløsing.
I norsk skole har det derimot vært lite systematisk arbeid med generelle strategier for problemløsing. Dette håper vi i Kikora at nå at er i ferd med å endre seg, siden arbeid med problemløsning er fremhevet i gjeldende læreplan LK-20: Her påpekes det at «elevene skal bli gode problemløsere og forstå hvordan matematikk henger sammen med andre fag».
Undervisning i problemløsing - to ulike tilnærminger.
Elever som får eksplisitt undervisning i sentrale matematiske problemløsningsmetoder blir bedre problemløsere enn elevene som får tradisjonell undervisning.
- Tilbake til den den tradisjonelle undervisningen Hallgeir beskrev tidligere. Her er det normalt at fokuset rettes mot selve aktiviteten eller oppgaven elevene skal arbeide med. Selve metoden – altså måten å angripe problemet på – blir sjelden eller aldri gjenstand for spesiell oppmerksomhet.
- Skal vi ta arbeidet med problemløsing på alvor må målet for timen knyttes til selve strategien. Kikoras problemløserskole er strukturert rundt seks ulike metoder for problemløsning. Gjennom utvalgte oppgaver presenteres disse metodene og elevene får erfaringer med når de kan være nyttig å bruke. Skal man lykkes med en slik tilnærming, settes det krav til valg av hvilke problem vi skal presentere og jobbe med. (Amit og Portnov-Naaman, 2017) «Problemet må være slik at den aktuelle strategien blir et naturlig valg – i alle fall for noen av elevene.». (Johnson; Herr & Kysh, 2004)

I Kikora mener vi elevene bør lære seg disse seks ulike metodene for problemløsing, og opplæringen i disse bør starte tidlig i skolegangen. Etter at elevene har gjennomført opplæringen i Problemløserskolen, kommer et eget kapittel som heter «Blandet». Dette er en oppgavesamling med gode oppgaver hvor elevene sammen med lærer kan diskutere seg frem til ulike måter å angripe problemet på. Når vi beskriver disse oppgavene som gode, er det fordi de kjennetegnes ved at:
- oppgavene fokuserer på å utvikle forståelse for matematiske begreper og ideer
- de antyder brede og generelle strategier for å finne en løsning,
- oppgavene fokuserer ikke på algoritmer som kan være et hinder for å utvikle begrepsmessig forståelse
- oppgavene krever en form for selvregulering av elevenes eget arbeid
- elevene må ta i bruk relevant forkunnskap og erfaring og finne en måte å bruke kunnskapen de allerede har i arbeidet med oppgaven
(Anita Valenta, Matematikksenteret, 2016)
Problemløserskolen og vertikale tavler
Målet med Kikoras problemløserskole er at elevene skal kjenne til disse seks metodene for problemløsning. Så ser vi at når elevene har jobbet med disse metodene over tid, så setter de sammen deler av de ulike metodene til sine egne problemløsningsstrategier. Det å kunne kombinere flere metoder og jobbe med matematiske problemer over tid danner grunnlag for utviklingen av egne strategier.
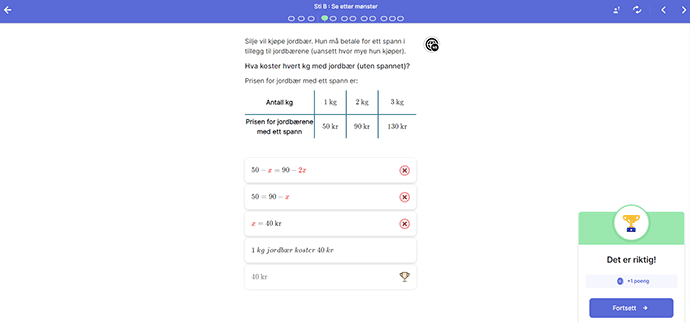
Kikoras problemløserskole er derfor for alle elever, uansett nivå, fordi elevene får representere problemet med «sitt eget språk» (for eksempel oversette fra tekst til tegning) og det viser seg at metodene har et stort bruksområde.
Så tilbake til Hallgeirs refleksjonsspørsmål nevnt tidligere: «Hvor stor del av en tradisjonell time har elevene fått mulighet til å tenke selv?» Peter Liljedahl har med sin forskning rundt «Building thinking classrooms», møtt stor interesse fra forskere og lærere over hele verden (https://buildingthinkingclassrooms.com/).
I sin forskning er Liljedahl opptatt av hvilke oppgaver elevene jobber med, og hvordan læreren veileder elevene. Han har også jobbet mye med hvordan arbeidsmetodene påvirker elevenes tenking og læring. Ett av Liljedahls mest kjente funn, er at når elever jobber stående ved whiteboard-tavler eller lignende (vertikale tavler), oppstår det mer engasjement, diskusjon og deltagelse I klasserommet. På sin hjemmeside, beskriver han metodikken i sin helhet, men Hallgeir mener at man bør begynne i det små. For hans egen del handler det mye om disse tre punktene:
- Oppgaver som fremmer tenking, ikke kopiering
- Tilfeldig sammensatte grupper som endres ofte
- Bruk vertikale ikke-permanente tavler
De øvrige 11 punktene Liljedahl beskriver, kan komme etter hvert.
Deltakerne fikk så gjøre seg kjent med Kikoras problemløserskole, før det var tid for å jobbe videre med noen av Hallgeirs utvalgte problemer. Deltakerne ble valgt i tilfeldige grupper via denne nettsiden (https://www.classtools.net/random-group-generator/), så var det bare å reise seg opp å begynne å løse problemer på Hallgeirs vertikale tavler. Disse tavlene sammen med tusjer kan man få kjøpt på f.eks. Clas Ohlson (https://www.clasohlson.com/no/Selvheftende-whiteboardfilm-60-x-80-cm/p/44-1717)